Enrichment

V-categories(2)
V-category(1)

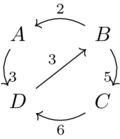
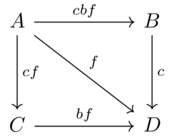
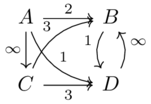
A \(\mathcal{V}\) category, given a symmetric monoidal preorder \(\mathcal{V}=(V,\leq,I,\otimes)\)

  • To specify the category \(\mathcal{X}\), one specifies:

    1. A set \(Ob(\mathcal{X})\) whose elements are called objects

    2. A hom-object for every pair of objects in \(Ob(\mathcal{X})\), written \(\mathcal{X}(x,y) \in V\)

  • The following properties must be satisfied:

    1. \(\forall x \in Ob(\mathcal{X}):\) \(I \leq \mathcal{X}(x,x)\)

    2. \(\forall x,y,z \in Ob(\mathcal{X}):\) \(\mathcal{X}(x,y)\otimes\mathcal{X}(y,z) \leq \mathcal{X}(x,z)\)

  • We call \(\mathcal{V}\) the base of enrichment for \(\mathcal{X}\) or say that \(\mathcal{X}\) is enriched in \(\mathcal{V}\).

Linked by

Bool-category(1)

  • Consider the following preorder:

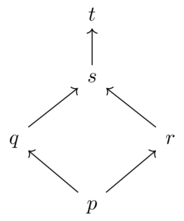
  • As a Bool-category, the objects are \(Ob(\mathcal{X})=\{p,q,r,s,t\}\).

    • For every pair, we need an element of Bool, so make it true if \(x\leq y\)

    • \(true\) is the monoidal unit of Bool, and this obeys the two constraints of a \(\mathcal{V}\) category.

  • We can represent the binary relation (hom-object) with a table:

    \(\leq\) p q r s t
    p T T T T T
    q F T F T T
    r F F T T T
    s F F F T T
    t F F F F T

Preorders as Bool-categories(2)
Preorders are Bool-categories(2)

There is a one-to-one correspondence between preorders and Bool-categories

Proof(1)

  • Construct preorder \((X,\leq_X)\) from any Bool-category \(\mathcal{X}\)

    • Let \(X\) be \(Ob(\mathcal{X})\) and \(x\ \leq_X\ y\) be defined as \(\mathcal{X}(x,y)=true\)

    • This is reflexive and transitive because of the two constraints we put on enriched categories.

      • The first constraint says that \(true \leq (x \leq_X x)\)

      • The second constraint says \((x \leq_X y) \land (y \leq_X z) \leq (x \leq_X z)\)

  • Construct Bool-category from a preorder:

    • Let \(Ob(X)=X\) and define \(\mathcal{X}(x,y)=true\) iff \(x \leq_X y\)

    • The two constraints on preorders give us our two required constraints on enriched categories.

Lawvere metric spaces(10)
Metric space(1)

A metric space \((X,d)\)

  • A set \(X\) whose elements are called points

  • A function \(X \times X \xrightarrow{d} \mathbb{R}_{\geq 0}\) which gives the distance between two points.

  • These must satisfy three properties:

    1. \(d(x,y)=0 \iff x=y\)

    2. \(d(x,y)=d(y,x)\)

    3. \(d(x,y)+d(y,z)\geq d(x,z)\) (triangle inequality)

  • An extended metric space includes \(\infty\) in the codomain of the cost function.

Linked by

Lawvere metric space(1)

A Lawvere metric space

  • A Cost-category, i.e. a category enriched in the symmetric monoidal preorder \(\mathbf{Cost}=([0,\infty],\geq,0,+)\).

  • \(X\) is given as \(Ob(\mathcal{X})\)

  • \(d(x,y)\) is given as \(\mathcal{X}(x,y)\)

  • The axiomatic properties of a category enriched in Cost are:

    • \(0 \geq d(x,x)\)

    • \(d(x,y)+d(y,z) \geq d(x,z)\)

Linked by

Reals metric space(1)

The set \(\mathbb{R}\) can be given a metric space structure, with \(d(x,y)=|x-y|\).

Exercise 2-52(2)

  • Imagine the points of a metric space are whole regions, like US, Spain, and Boston. Distance is "Given the worst case scenario, how far do you have to travel to get from region A to B?"

  • This actually breaks our symmetry requirement: \(d(Boston,US)=0, d(US,Boston) > 0\)

  • Which distance is bigger in this framework: \(d(Spain,US)\) or \(d(US,Spain)\)?

Solution(1)

  • \(d(US,Spain)\) is bigger because there is much more room for the worst case scenario to place one farther for Spain.

  • A bigger first argument makes things strictly worse, all else equal. A bigger second argument makes things strictly better, all else equal.

Linked by

Exercise 2-55(2)

Consider the symmetric monoidal preorder \((\mathbb{R},\geq,0,+)\) which is the same as Cost but does not include \(\infty\). How do you characterize the difference between this and a Lawvere metric space in the sense of definition 2.46?

Solution(1)

It is a metric space in which points may only be finitely-far apart.

Exercise 2-60(2)

What is the distance matrix represented by this graph?

Solution(1)
\(\rightarrow\) A B C D
A 0 6 3 11
B 2 0 5 5
C 5 3 0 8
D 11 9 6 0

Linked by

V-variations on preorders and metric spaces(6)
Exercise 2-61(2)

Recall the symmetric monoidal preorder \(\mathbf{NMY} := (P,\leq, yes, min)\) from Exercise 2.34. Interpret what a NMY-category is.

Solution(1)

It is like a graph where some edges are ‘maybe’ edges. We can ask the question “Is there a path from a to b?" and if there is a true path we will get a ‘yes’. If the only paths are those which include maybe edges, then we get a ’maybe’. If there’s no path at all, we get a ‘no’.

Exercise 2-62(2)

  • Let \(M\) be a set and \(\mathcal{M}:=(P(M),\subseteq, M, \cap)\) be the symmetric monoidal preorder whose elements are subsets of \(M\).

  • Someone says "for any set \(M\), imagine it as the set of modes of transportation (e.g. car, boat, foot)". Then an \(\mathcal{M}\) category \(\mathcal{X}\) tells you all the modes that will get you from a all the way to b, for any two points \(a,b \in Ob(\mathcal{X})\)

    1. Draw a graph with four vertices and five edges, labeled with a subset of \(M=\{car,boat,foot\}\)

    2. From this graph it is possible to construct an \(\mathcal{M}\) category where the hom-object from x to y is the union of the sets for each path from x to y, where the set of a path is the intersection of the sets along the path. Write out the corresponding 4x4 matrix of hom-objects and convince yourself this is indeed an \(\mathcal{M}\) category.

    3. Does the person’s interpretation look right?

Solution(1)

  1. (implicitly, no path means edge of \(\varnothing\) and self paths are \(cfb\))

  2. Hom objects:

    A B C D
    A cbf cbf cf cf
    B \(\varnothing\) cbf \(\varnothing\) c
    C \(\varnothing\) \(\varnothing\) cbf bf
    D \(\varnothing\) \(\varnothing\) \(\varnothing\) cbf

    • The first property (\(\forall x \in Ob(\mathcal{X}): I \leq \mathcal{X}(x,x)\)) is satisfied by noting the diagonal entries are equal to the unit.

    • The second property (\(\forall x,y,z \in Ob(\mathcal{X}): \mathcal{X}(x,y)\otimes\mathcal{X}(y,z) \leq \mathcal{X}(x,z)\)) can be checked looking at the following cases:

      • \(A \rightarrow B \rightarrow D\): \(cbf \cap c \leq cf\)

      • \(A \rightarrow C \rightarrow D\): \(cf \cap bf \leq cf\)

  3. One subtlety is that we need to say that one can get from any place to itself by any means of transportation for this to make sense. Overall interpretation looks good.

Exercise 2-63(2)

Consider the symmetric monoidal preorder \(\mathcal{W}:=(\mathbb{N}\cup\{\infty\},\leq,\infty,min)\)

  1. Draw a small graph labeled by elements of \(\mathbb{N}\cup\{\infty\}\)

  2. Write a the matrix whose rows and columns are indexed by nodes in the graph, whose (x,y)th entry is given by the maximum over all paths p from x to y of the minimum edge label in p.

  3. Prove that this matrix is a matrix of hom-objects for a \(\mathcal{W}\) category called \(\mathcal{X}\).

  4. Make up an interpretation for what it means to enrich in \(\mathcal{W}\)

Solution(1)

  1. (implicitly, no path means path of weight 0, and self paths have weight \(\infty\))

  2. Maxmin matrix:

    A B C D
    A \(\infty\) 3 \(\infty\) 3
    B 0 \(\infty\) 0 \(\infty\)
    C 0 3 \(\infty\) 3
    D 0 1 0 \(\infty\)

    Self paths are equal to the monoidal unit and it will never be the case that \(min(\mathcal{X}(A,B),\mathcal{X}(B,C)) > \mathcal{X}(A,C)\) because even in the worst-case scenario (where there is not a better path from A to C that ignores B completely), we form the best path by combining the best path from A to B with the best from B to C. We are forced to take the minimum edge label in the path, which means that the lowest \(\mathcal{X}(A,C)\) can be is actually equal to the left hand side.

  3. The edges could represent constraints (\(\infty\) is fully unconstrained, \(0\) is fully constrained, e.g. the diameter of a pipe) and the hom-object represents the least-constrained thing that can get from one point to another. The monoidal unit says that something can be fully unconstrained if it stays where it is, and the monoidal product (min) says how to compose two different constraints in series.